PyCurve - Python Yield Curve Toolkit

What is it ?

PyCurve is a Python package that provides to user high level
yield curve usefull tool. For example you can istanciate a Curve
and get a d_rate, a discount factor, even forward d_rate given multiple
methodology from Linear Interpolation to parametrization methods
as Nelson Siegel or Bjork-Christenssen. PyCurve is also able to provide
solutions in order to build yield curve or price Interest rates derivatives
via Vasicek or Hull and White.

Features

Below this is the features that this package tackle :

Curve Smoothing:
- Create Curve Object with two numpy array (t,rt)
- Linear interpolation given a Curve
- Cubic interpolation given a Curve
- Nelson Siegel and Svensson model creation and components plotting
- Nelson Siegel and Svensson calibration given a Curve
- Bjork Christensen and Augmented (6 factors) model creation and components plotting
Stochastic Modelling:
- Vasicek Model Simulation
- Hull and White one factor Model Simulation

How to install

From pypi

pip install PyCurve

From pypi specific version

pip install PyCurve==0.0.5

From Git

git clone https://github.com/ahgperrin/PyCurve.git
pip install -e .

Objects

Curve Object

This object consists in a simple yield curve encapsulation. This object is used by others class to encapsulate results
or in order to directly create a curve with data obbserved in the market.

Attributes	Type	Description
rt	Private	Interest rates as float in a numpy.ndarray
t	Private	Time as float or int in a numpy.ndarray

Methods	Type	Description	Return
get_rate	Public	rt getter	_rt
get_time	Public	rt getter	_t
set_rate	Public	rt getter	None
set_time	Public	rt getter	None
is_valid_attr(attr)	Private	Check attributes validity	attribute
plot_curve()	Public	Plot Yield curve	None

Example

from PyCurve.curve import Curve
time = np.array([0.25, 0.5, 0.75, 1., 2., 
        3., 4., 5., 10., 15., 
        20.,25.,30.])
rate = np.array([-0.63171, -0.650322, -0.664493, -0.674608, -0.681294,
        -0.647593, -0.587828, -0.51251, -0.101804,  0.182851,
        0.32962,0.392117,  0.412151])
curve = Curve(rate,time)
curve.plot_curve()
print(curve.get_rate)
print(curve.get_time)

[ 0.25  0.5   0.75  1.    2.    3.    4.    5.   10.   15.   20.   25.
 30.  ]
[-0.63171  -0.650322 -0.664493 -0.674608 -0.681294 -0.647593 -0.587828
 -0.51251  -0.101804  0.182851  0.32962   0.392117  0.412151]

Simulation Object

This object consists in a simple simulation encapsulation. This object is used by others class to encapsulate results
of monte carlo simulation. This Object has build in method that could perform the conversion from a simulation to
a yield curve or to a discount factor curve.

Attributes	Type	Description
sim	Private	Simulated paths matrix numpy.ndarray
dt	Private	delta_time as float or int in a numpy.ndarray

Methods	Type	Description & Params	Return
get_sim	Public	sim getter	_rt
get_nb_sim	Public	nb_sim getter	sim.shape[0]
get_steps	Public	steps getter	sim.shape[1]
get_dt	Public	dt getter	_dt
is_valid_attr(attr)	Private	Check attributes validity	attribute
yield_curve()	Public	Create a yield curve from simulated paths	Curve
discount_factor()	Public	Convert d_rate simulation to discount factor	np.ndarray
plot_discount_curve(average)	Public	Plot discount factor (average :bool False plot all paths True Plot estimate)	None
plot_simulation()	Public	Plot Yield curve	None
plot_yield_curve()	Public	Plot Yield curve	None
plot_model()	Public	Plot Yield curve	None

Example

Using Vasicek to Simulate

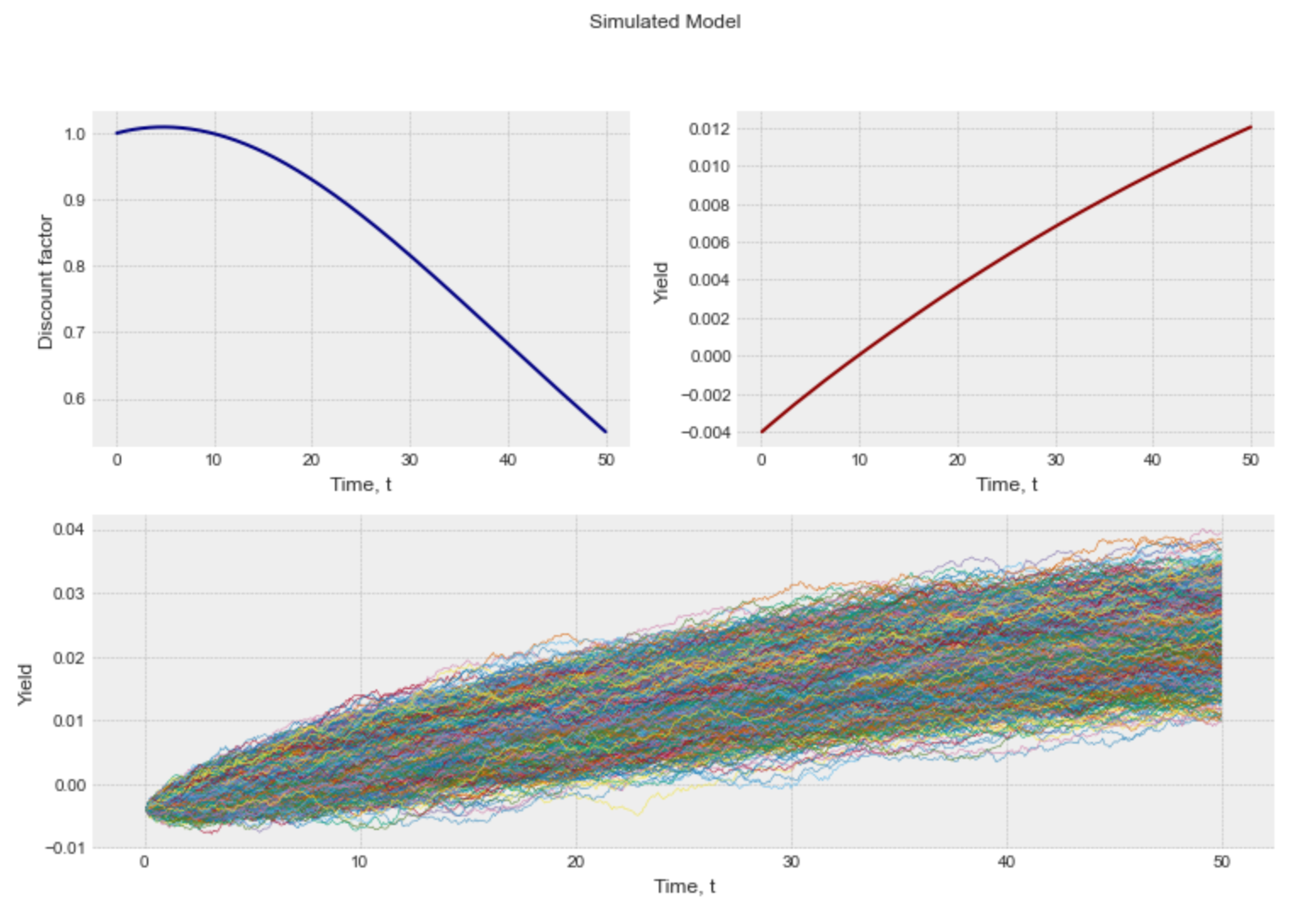
from PyCurve.vasicek import Vasicek
vasicek_model = Vasicek(0.02, 0.04, 0.001, -0.004, 50, 30 / 365)
simulation = vasicek_model.simulate_paths(2000) #Return a Simulation and then we can apply Simulation Methods
simulation.plot_yield_curve()

simulation.plot_model()

Yield Curve Construction Tools

This section is the description with examples of what you can do with this package
Please note that for all the examples in this section curve is referring to the curve below
you can see example regarding Curve Object in the dedicated section.

from PyCurve import Curve
time = np.array([0.25, 0.5, 0.75, 1., 2., 
        3., 4., 5., 10., 15., 
        20.,25.,30.])
d_rate = np.array([-0.63171, -0.650322, -0.664493, -0.674608, -0.681294,
        -0.647593, -0.587828, -0.51251, -0.101804,  0.182851,
        0.32962,0.392117,  0.412151])
curve = Curve(time,d_rate)

linear

Interpolate any d_rate from a yield curve using linear interpolation. THis module is build using scipy.interpolate

Attributes	Type	Description
curve	Private	Curve Object to be intepolated
func_rate	Private	interp1d Object used to interpolate

Methods	Type	Description & Params	Return
d_rate(t)	Public	d_rate interpolation t: float, array,int	float
df_t(t)	Public	discount factor interpolation t: float, array,int	float
forward(t1,t2)	Public	forward d_rate between t1 and t2 t1,t2: float, array,int	float
create_curve(t_array)	Public	create a Curve object for t values t:array	Curve
is_valid_attr(attr)	Private	Check attributes validity	attribute

Example

from PyCurve.linear import LinearCurve
linear_curve = LinearCurve(curve)
print("7.5-year d_rate : "+str(linear_curve.d_rate(7.5)))
print("7.5-year discount d_rate : "+str(linear_curve.df_t(7.5)))
print("Forward d_rate between 7.5 and 12.5 years : "+str(linear_curve.forward(7.5,12.5)))

7.5-year d_rate : -0.307157
7.5-year discount d_rate : 1.0233404498400862
Forward d_rate between 7.5 and 12.5 years : 0.5620442499999999

cubic

Interpolate any d_rate from a yield curve using linear interpolation. THis module is build using scipy.interpolate

Attributes	Type	Description
curve	Private	Curve Object to be intepolated
func_rate	Private	PPoly Object used to interpolate

Methods	Type	Description & Params	Return
d_rate(t)	Public	d_rate interpolation t: float, array,int	float
df_t(t)	Public	discount factor interpolation t: float, array,int	float
forward(t1,t2)	Public	forward d_rate between t1 and t2 t1,t2: float, array,int	float
create_curve(t_array)	Public	create a Curve object for t values t:array	Curve
is_valid_attr(attr)	Private	Check attributes validity	attribute

Example

from PyCurve.cubic import CubicCurve
cubic_curve = CubicCurve(curve)
print("10-year d_rate : "+str(cubic_curve.d_rate(7.5)))
print("10-year discount d_rate : "+str(cubic_curve.df_t(7.5)))
print("Forward d_rate between 10 and 20 years : "+str(cubic_curve.forward(7.5,12.5)))

10-year d_rate : -0.3036366057950627
10-year discount d_rate : 1.0230694659050514
Forward d_rate between 10 and 20 years : 0.6078001168478189

Nelson-Siegel

Attributes	Type	Description
beta0	Private	Model Coefficient Beta0
beta1	Private	Model Coefficient Beta1
beta2	Private	Model Coefficient Beta2
tau	Private	Model Coefficient tau
attr_list	Private	Coefficient list

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
set_attr(attr)	Public	attributes setter	None
print_model()	Public	print the Ns model set	None
_calibration_func(x,curve)	Private	Private method used for calibration method	float:sqr_err
_is_positive_attr(attr)	Private	Check attributes positivity (beta0 and tau	attribute
_is_valid_curve(curve)	Private	Check if the curve given for calibration is a Curve Object	Curve
_print_fitting()	Private	Print the result after the calibration	None
calibrate(curve)	Public	Minimize _calibration_func(x,curve)	sco.OptimizeResult
_time_decay(t)	Private	Compute the time decay part of the model t (float or array)	float,array
_hump(t)	Private	Compute the hump part of the model given t (float or array)	float,array
d_rate(t)	Public	Get d_rate from the model for a given time t (float or array)	float,array
plot_calibrated()	Public	Plot Model curve against Curve	None
plot_model_params()	Public	Plot Model parameters	None
plot_model()	Public	Plot Model Components	None
df_t(t)	Public	Get the discount factor from the model for a given time t (float or array)	float,array
cdf_t(t)	Public	Get the continuous df from the model for a given time t (float or array)	float,array
forward_rate(t1,t2)	Public	Get the forward d_rate for a given time t1,t2 (float or array)	float,array

Example

Creation of a model and calibration

from PyCurve.nelson_siegel import NelsonSiegel
ns = NelsonSiegel(0.3,0.4,12,1)
ns.calibrate(curve)

Nelson Siegel Model
============================
beta0 = 0.751506062319988
beta1 = -1.3304971868997248
beta2 = -2.2203178895179176
tau = 2.5493056203052005
____________________________
============================
Calibration Results
============================
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
Mean Squared Error 0.0042367306926415285
Number of Iterations 20
____________________________
Out[19]:
      fun: 0.0042367306926415285
 hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
      jac: array([-2.40077054e-06,  9.51322360e-07, -2.33927462e-07,  7.97278914e-07])
  message: 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
     nfev: 105
      nit: 20
     njev: 21
   status: 0
  success: True
        x: array([ 0.75150606, -1.33049719, -2.22031789,  2.54930562])

Plotting and analyse

ns.plot_calibrated()

ns.plot_model_params()

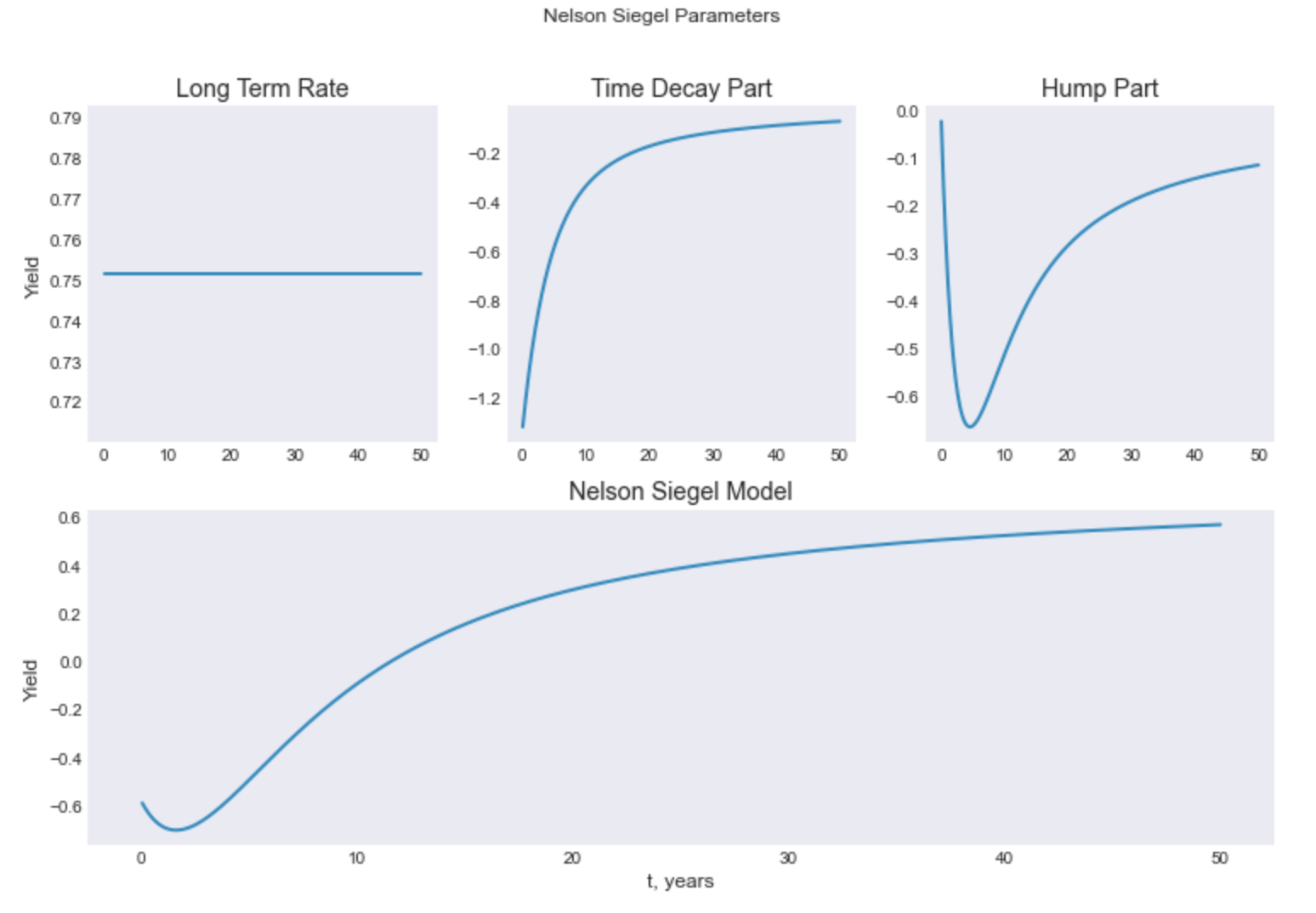
ns.plot_model()

nelson-siegel-svensson

Attributes	Type	Description
beta0	Private	Model Coefficient Beta0
beta1	Private	Model Coefficient Beta1
beta2	Private	Model Coefficient Beta2
beta3	Private	Model Coefficient Beta3
tau	Private	Model Coefficient tau
tau2	Private	Model Coefficient tau2
attr_list	Private	Coefficient list

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
set_attr(attr)	Public	attributes setter	None
print_model()	Public	print the Ns model set	None
_calibration_func(x,curve)	Private	Private method used for calibration method	float:sqr_err
_is_positive_attr(attr)	Private	Check attributes positivity (beta0 and tau	attribute
_is_valid_curve(curve)	Private	Check if the curve given for calibration is a Curve Object	Curve
_print_fitting()	Private	Print the result after the calibration	None
calibrate(curve)	Public	Minimize _calibration_func(x,curve)	sco.OptimizeResult
_time_decay(t)	Private	Compute the time decay part of the model t (float or array)	float,array
_hump(t)	Private	Compute the hump part of the model given t (float or array)	float,array
_second_hump(t)	Private	Compute the second hump part of the model given t (float or array)	float,array
d_rate(t)	Public	Get d_rate from the model for a given time t (float or array)	float,array
plot_calibrated()	Public	Plot Model curve against Curve	None
plot_model_params()	Public	Plot Model parameters	None
plot_model()	Public	Plot Model Components	None
df_t(t)	Public	Get the discount factor from the model for a given time t (float or array)	float,array
cdf_t(t)	Public	Get the continuous df from the model for a given time t (float or array)	float,array
forward_rate(t1,t2)	Public	Get the forward d_rate for a given time t1,t2 (float or array)	float,array

Example

Creation of a model and calibration

from PyCurve.svensson_nelson_siegel import NelsonSiegelAugmented
nss = NelsonSiegelAugmented(0.3,0.4,12,12,1,1)
nss.calibrate(curve)

Augmented Nelson Siegel Model
============================
beta0 = 0.7515069899513361
beta1 = -1.3304984652740972
beta2 = -1.3582175270153745
beta3 = -0.8621237370245594
tau = 2.5492666085730384
tau2 = 2.5493745447283485
____________________________
============================
Calibration Results
============================
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
Mean Squared Error 0.004236730702075479
Number of Iterations 31
____________________________
Out[31]:
      fun: 0.004236730702075479
 hess_inv: <6x6 LbfgsInvHessProduct with dtype=float64>
      jac: array([-8.70041881e-06, -3.48375844e-06, -1.71824361e-06, -1.71911096e-06,
        1.00535900e-06,  3.23178986e-07])
  message: 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
     nfev: 245
      nit: 31
     njev: 35
   status: 0
  success: True
        x: array([ 0.75150699, -1.33049847, -1.35821753, -0.86212374,  2.54926661,
        2.54937454])

Plotting possibilities are the same as for the Nelson-Siegel model for example

nss.plot_model_params()

bjork-christensen

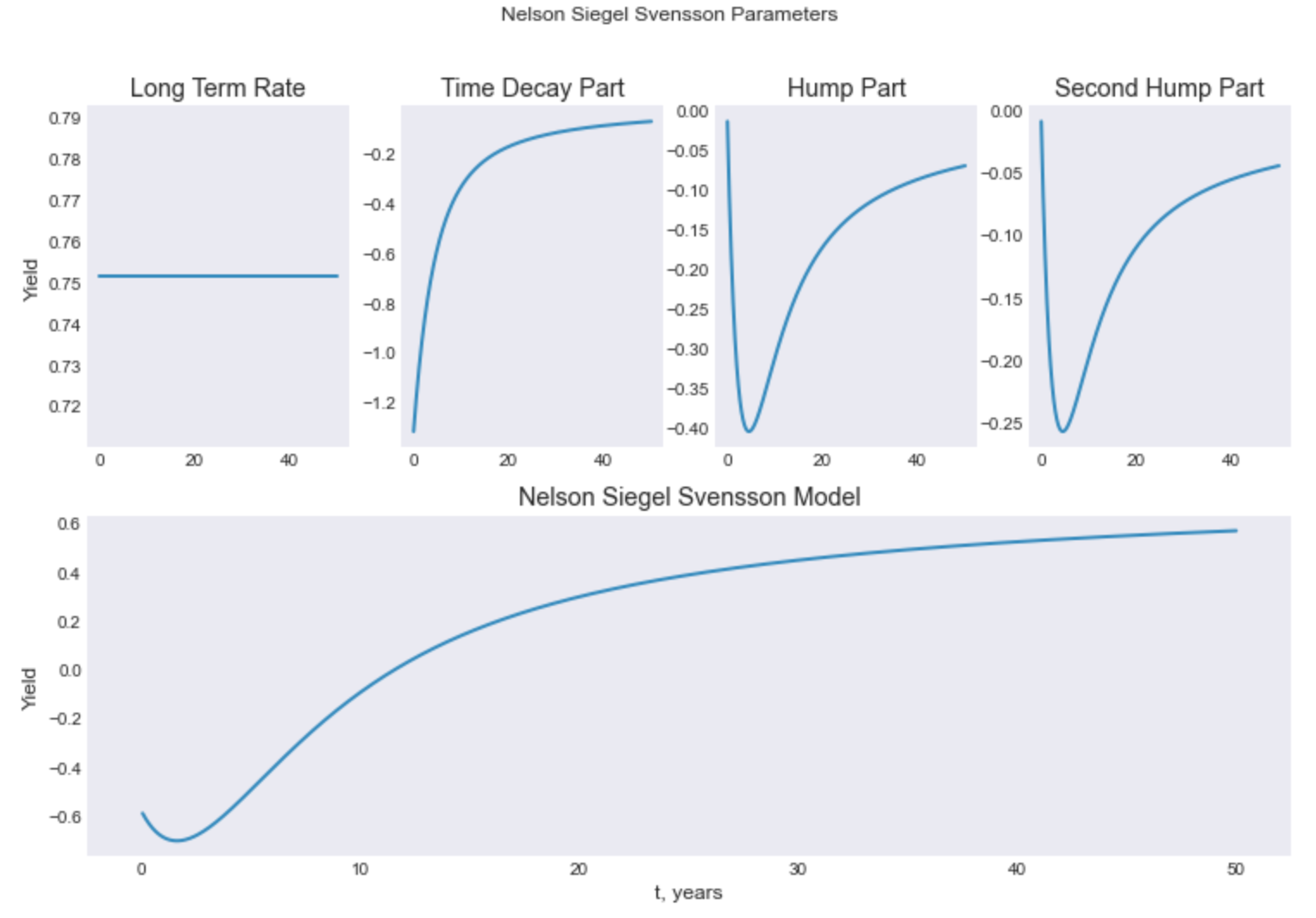
Attributes	Type	Description
beta0	Private	Model Coefficient Beta0
beta1	Private	Model Coefficient Beta1
beta2	Private	Model Coefficient Beta2
beta3	Private	Model Coefficient Beta3
tau	Private	Model Coefficient tau
attr_list	Private	Coefficient list

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
set_attr(attr)	Public	attributes setter	None
print_model()	Public	print the Ns model set	None
_calibration_func(x,curve)	Private	Private method used for calibration method	float:sqr_err
_is_positive_attr(attr)	Private	Check attributes positivity (beta0 and tau	attribute
_is_valid_curve(curve)	Private	Check if the curve given for calibration is a Curve Object	Curve
_print_fitting()	Private	Print the result after the calibration	None
calibrate(curve)	Public	Minimize _calibration_func(x,curve)	sco.OptimizeResult
_time_decay(t)	Private	Compute the time decay part of the model t (float or array)	float,array
_hump(t)	Private	Compute the hump part of the model given t (float or array)	float,array
_second_hump(t)	Private	Compute the second hump part of the model given t (float or array)	float,array
d_rate(t)	Public	Get d_rate from the model for a given time t (float or array)	float,array
plot_calibrated()	Public	Plot Model curve against Curve	None
plot_model_params()	Public	Plot Model parameters	None
plot_model()	Public	Plot Model Components	None
df_t(t)	Public	Get the discount factor from the model for a given time t (float or array)	float,array
cdf_t(t)	Public	Get the continuous df from the model for a given time t (float or array)	float,array
forward_rate(t1,t2)	Public	Get the forward d_rate for a given time t1,t2 (float or array)	float,array

Example

Creation of a model and calibration

from PyCurve.bjork_christensen import BjorkChristensen
bjc = BjorkChristensen(0.3,0.4,12,12,1)
bjc.calibrate(curve)

Bjork & Christensen Model
============================
beta0 = 0.7241026361747042
beta1 = 1.2630412759302045
beta2 = -4.075775255903699
beta3 = -2.61578890758314
tau = 2.0454907238894267
____________________________
============================
Calibration Results
============================
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
Mean Squared Error 0.002575936865445517
Number of Iterations 37
____________________________
Out[36]:
      fun: 0.002575936865445517
 hess_inv: <5x5 LbfgsInvHessProduct with dtype=float64>
      jac: array([-1.34584183e-06,  7.22165387e-07, -9.63335320e-07,  1.34501786e-06,
        4.57750160e-07])
  message: 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL'
     nfev: 252
      nit: 37
     njev: 42
   status: 0
  success: True
        x: array([ 0.72410264,  1.26304128, -4.07577526, -2.61578891,  2.04549072])

Plotting possibilities are the same as for the Nelson-Siegel model for example

bjc.plot_model()

bjork-christensen-augmented

Attributes	Type	Description
beta0	Private	Model Coefficient Beta0
beta1	Private	Model Coefficient Beta1
beta2	Private	Model Coefficient Beta2
beta3	Private	Model Coefficient Beta3
beta4	Private	Model Coefficient Beta4
tau	Private	Model Coefficient tau
attr_list	Private	Coefficient list

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
set_attr(attr)	Public	attributes setter	None
print_model()	Public	print the Ns model set	None
_calibration_func(x,curve)	Private	Private method used for calibration method	float:sqr_err
_is_positive_attr(attr)	Private	Check attributes positivity (beta0 and tau	attribute
_is_valid_curve(curve)	Private	Check if the curve given for calibration is a Curve Object	Curve
_print_fitting()	Private	Print the result after the calibration	None
calibrate(curve)	Public	Minimize _calibration_func(x,curve)	sco.OptimizeResult
_time_decay(t)	Private	Compute the time decay part of the model t (float or array)	float,array
_hump(t)	Private	Compute the hump part of the model given t (float or array)	float,array
_second_hump(t)	Private	Compute the second hump part of the model given t (float or array)	float,array
_third_hump(t)	Private	Compute the third hump part of the model given t (float or array)	float,array
d_rate(t)	Public	Get d_rate from the model for a given time t (float or array)	float,array
plot_calibrated()	Public	Plot Model curve against Curve	None
plot_model_params()	Public	Plot Model parameters	None
plot_model()	Public	Plot Model Components	None
df_t(t)	Public	Get the discount factor from the model for a given time t (float or array)	float,array
cdf_t(t)	Public	Get the continuous df from the model for a given time t (float or array)	float,array
forward_rate(t1,t2)	Public	Get the forward d_rate for a given time t1,t2 (float or array)	float,array

Example

Creation of a model and calibration

from PyCurve.bjork_christensen_augmented import BjorkChristensenAugmented
bjc_a = BjorkChristensenAugmented(0.3,0.4,12,12,12,1)
bjc_a.calibrate(curve)

Bjork & Christensen Augmented Model
============================
beta0 = 1.5954945516202643
beta1 = -0.1362673420894012
beta2 = -1.921347491829477
beta3 = -3.100138400789165
beta4 = -0.2790540854856497
tau = 3.3831338085688625
____________________________
============================
Calibration Results
============================
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
Mean Squared Error 4.6222147406189135e-05
Number of Iterations 45
____________________________
Out[39]:
      fun: 4.6222147406189135e-05
 hess_inv: <6x6 LbfgsInvHessProduct with dtype=float64>
      jac: array([-3.13922277e-05, -1.14224797e-04, -3.47444433e-05,  2.07803821e-05,
        7.91378953e-06,  6.50288949e-06])
  message: 'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 357
      nit: 45
     njev: 51
   status: 0
  success: True
        x: array([ 1.59549455, -0.13626734, -1.92134749, -3.1001384 , -0.27905409,
        3.38313381])

Plotting possibilities are the same as for the Nelson-Siegel model for example

bjc_a.plot_calibrated(curve)

Stochastic Tools

vasicek

Attributes	Type	Description
alpha	Private	Model Coefficient alpha (mean reverting speed)
beta	Private	Model Coefficient Beta (long term mean)
sigma	Private	Short rate Volatility
rt	Private	Initial Short Rate
time	Params	Time in years
dt	Private	time for each period
steps	Private	calculated with dt & time as time/dt

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
sigma_part(n)	Private	compute n sigma part	float
mu_dt(rt)	Private	compute drift part	float
simulate_paths(n)	Public	Simulate n Short rate paths	np.ndarray
plot_calibrated(simul,curve)	Public	Plot yield curve against simulate curve	None

time = np.array([0.25, 0.5, 0.75, 1., 2.,
                 3., 4., 5., 10., 15.,
                 20., 25., 30.])
rate = np.array([-0.0063171, -0.00650322, -0.00664493, -0.00674608, -0.00681294,
                 -0.00647593, -0.00587828, -0.0051251, -0.00101804, 0.00182851,
                 0.0032962, 0.0030092117, 0.00412151])
curve = Curve(time,rate)
vasicek_model = Vasicek(0.5, 0.0040, 0.001, -0.0067, 30, 1 / 365)
simulation = vasicek_model.simulate_paths(200)
vasicek_model.plot_calibrated(simulation,curve)

All the tools for graphing from simulation could be applied to vasicek simulation results.

hull & white

Attributes	Type	Description
alpha	Private	Model Coefficient alpha (mean reverting speed)
sigma	Private	Short rate Volatility
rt	Private	Initial Short Rate
time	Params	Time in years
dt	Private	time for each period
steps	Private	calculated with dt & time as time/dt
f_curve	Private	Curve : Initial instantaneous forward structure
method	Private	method used in order to interpolate f_curve

Methods	Type	Description & Params	Return
get_attr(str(attr))	Public	attributes getter	attribute
_is_valid_curve(curve)	Private	Check if the curve given for calibration is a Curve Object	Curve
sigma_part(n)	Private	compute n sigma part	float
interp_forward(t)	Private	interpolate forward curve for maturity t	float
theta_part(t)	Private	compute theta(t)	float
mu_dt(rt,t)	Private	compute drift part at time t	float
simulate_paths(n)	Public	Simulate n Short rate paths	np.ndarray
plot_calibrated(simul)	Public	Plot yield curve against simulate curve	None

Example

from PyCurve.bjork_christensen_augmented import BjorkChristensenAugmented
from PyCurve.hull_white import HullWhite
import numpy as np
from PyCurve.curve import Curve
# Instance of curve : Spot Rates
time = np.array([0.25, 0.5, 0.75, 1., 2.,
                 3., 4., 5., 10., 15.,
                 20., 25., 30.])
rate = np.array([-0.0063171, -0.00650322, -0.00664493, -0.00674608, -0.00681294,
                 -0.00647593, -0.00587828, -0.0051251, -0.00101804, 0.00182851,
                 0.0032962, 0.00392117, 0.00412151])
curve = Curve(time, rate)
# Deduce Forward rate via Bjork Christensen (as example but you can directly create an instance of Curve with values)
bjc_a = BjorkChristensenAugmented(0.3, 0.4, 12, 12, 12, 1)
bjc_a.calibrate(curve)
forward_curve = [-0.006301821217413436379]
forward_curve_t = [0]
for i in range(12):
    forward_curve.append(bjc_a.forward_rate(time[i], time[i + 1]))
    forward_curve_t.append(time[i])
instantaneous_forward = Curve(forward_curve_t, forward_curve)
# Hull and white model  with High Volatility
hull_white_model = HullWhite(1, 0.02, -0.0063, 25, 1 / 365, instantaneous_forward, 'linear')
simulation = hull_white_model.simulate_paths(1000)
hull_white_model.plot_calibrated(simulation,curve)

Bjork & Christensen Augmented Model
============================
beta0 = 0.0003242320890548229
beta1 = 0.00042283628067360974
beta2 = 0.014729859086888815
beta3 = -0.03083749691652102
beta4 = -0.020626731632810553
tau = 1.137911384276111
____________________________
============================
Calibration Results
============================
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
Mean Squared Error 3.084012924460394e-06
Number of Iterations 24
____________________________

All the tools for graphing from simulation could be applied to Hull-White simulation results.

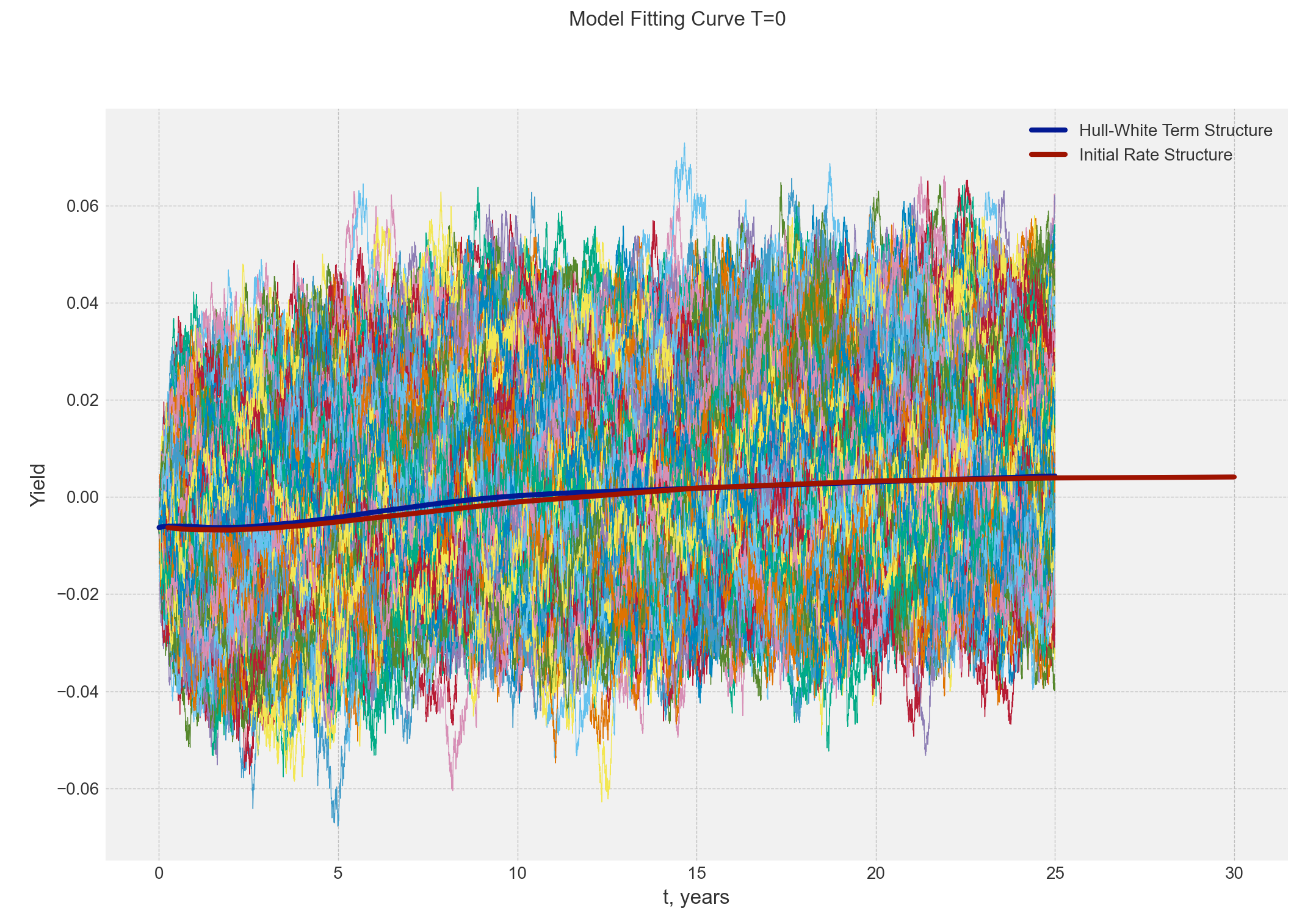
# Hull and white model  with High Volatility
hull_white_model_low_vol = HullWhite(1, 0.00002, -0.0063, 25, 1 / 365, instantaneous_forward, 'cubic')
simulation = hull_white_model_low_vol.simulate_paths(1000)
simulation.plot_model()
hull_white_model_low_vol.plot_calibrated(simulation,curve)