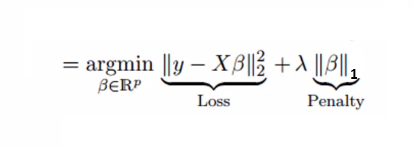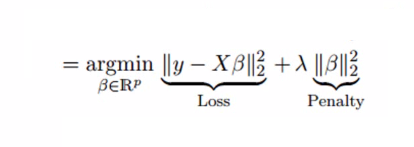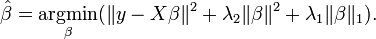Lasso-Ridge-Regression-and-Elastic_Net-Regularization-from-Scratch

Feature Selection:

We want to have a minimal number of eatures that it takes to really capture the trends and patterns of our data.

*NOTE:
Features != Information

Why do we do Feature Selection?

• It enables the machine learning algorithm to train faster.
• It reduces the complexity of a model and makes it easier to interpret.
• It improves the accuracy of a model if the right subset is chosen.

Regularization:

• This is the method for automatically penalizing extra features.
• It can set the coefficient of a feature to zero.

There are some pre-defined modules/libraries in sklearn that helps us in Reglarization/Feature Selection.

1. Lasso Regression
2. Ridge Regression
3. Elasric-Net Regularization

Lasso Regression:

• In Lasso Regression, we add Mean Absolute Value of coefficients.
• Lasso regression can completely eliminate the variable by reducing its coefficient value to 0.
• The new term we added to Ordinary Least Square(OLS) is called L1 Regularization.

  Formula:

  
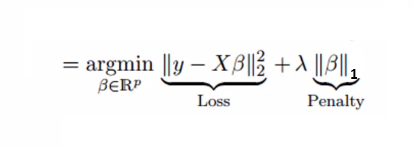
  The second term is basically a paramter with the term that describes how many features we are using.

Plotting Lasso Regression’s Coefficient Score:

Documentation of LASSO:

https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html

Ridge Regression:

• In Ridge Regression, we add Mean Square Values of coefficients.
• This term is the sum of squares of coefficient multiplied by the parameter.
• The motive of adding this term is to penalize the variable corresponding to that coefficient not very much correlated to the target variable.

  Formula:

  
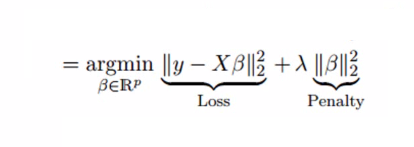
  In this equation, we have two components. First one is least square term and other one is lambda of the summation of β2 (beta- square) where β is the coefficient. This is added to least square term in order to shrink the parameter to have a very low variance.

Plotting Ridge Regression’s Coefficient Score:

Documentation of RIDGE:

https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html

Elastic-Net Regularizatoin:

• ElasticNet is hybrid of Lasso and Ridge Regression techniques.
• It is trained with L1 and L2 prior as regularizer.
• Elastic-net is useful when there are multiple features which are correlated. Lasso is likely to pick one of these at random, while elastic-net is likely to pick both.

Formula:

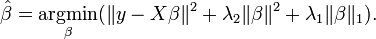
In elastic Net Regularization we added the both terms of L1 and L2 to get the final loss function.

Plotting Elastic-Net Regularization’s Coefficient Score:

Documentation of ELASTIC-NET:

https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html