A Javascript library for the demonstration of Euclidean shape reconstruction via Rips Complexes
The purpose of this webapp is to demonstrate a topological method for
Euclidean shape reconstrcution. The method has been developed as part of my PhD thesis.
See the paper: https://arxiv.org/abs/1810.10144.
The webapp runs on any modern web-browser on any stardard device.
This webapp does not require any extra installation besides a modern
web-browser. Hit the url https://www.smajhi.com/shape-reconstruction from your
favorite browser to open it. The app runs client-side Javascritpt for all the
computations, so you may need to enable JS engine in your browser if not already
enabled. The supported browsers include Google Chrome (>=48.0), Firefox
(>=65.0), Opera, and Safari. All the above mentioned browsers run JS by
default. The supported devices include Desktop, Laptop, Tablet, and
Phones. Since computation of Rips complexes involves quadratic time operations,
the app uses a ton of system CPU and RAM when the a large sample is chosen. For
this reason, we strongly discourage the users to run the application on their
phones or similar devices with very limited computational resources.
Altough the webapp is built keeping the Euclidean (2D) shape reconstruction in
mind, it can also be used to demontrate random sampling of a shape,
Vietoris-Rips complexes, and vusualization of Hausdorff distance. We discuss
below the features (so far) in detail.
The homepage consists of a navigation menu on top, below it are a white canvas
on the left and selection tools on the right side.

The canvas is the place where all visualizations take place. The selection tools
to its right is the main user input section, where four of its subsections are
stacked vertically. Each subsection is discussed below.
This input tool lets the user select a shape from the dropdown menu shown
below: Except for the first option, choosing other shapes immediately draws
the selected shape on the canvas. The choices include the Euclidean plane,
circle, lissajous, and lemniscate. The last two of the shapes are examples of
non-manifolds. We demonstrate the gemetric reconstruct this shape from a
randowm sample, which we are going to select next. The selected shape is used
as a reference in order to check the quality of our reconstruction.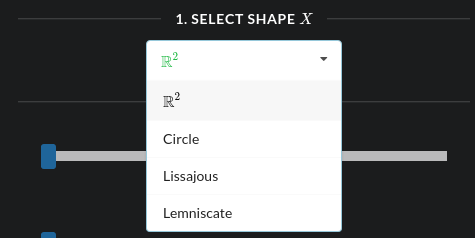
Once a shape has been chosen in step 1, it’s time to draw a sample from it.
The sample size and noise is chosen using the sliders. Finally, pressing the
sample button selects a random sample around the shape and draws the sample
points on the canvas. Add a positive noise to see the random sampling in
action a every time the “Sample” button is pressed.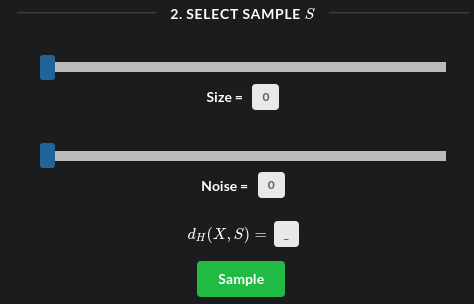
An “event listener” is keenly waiting to compute and draw the Vietoris-Rips
complex whenever any “change” of scale takes place on the slider. It’s
actually the “shadow” of the computed Rips complex that is drawn, also the
adjacency matrix of the 1-skeleton the the complex is stored for future use. A
large sample size may slow down the computation, so please wait a couple
of seconds after clicking on the slider if nothing shows up on the canvas.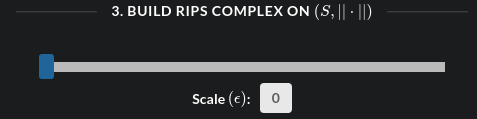
The toggle icon on the right of the top menu toggles the sidebar, which
contains different settings of the application.
This project is licensed under the MIT License; read
LICENSE.